Bernoulli’s Theorem and Its Applications

Introduction

Fluid dynamics is a cornerstone of engineering, physics, and several natural sciences. Among the various principles governing fluid behavior, Bernoulli’s Theorem holds a special place. This fundamental concept explains the interrelationship between pressure, velocity, and elevation in a moving fluid. Whether it’s the flight of airplanes or the operation of carburetors, Bernoulli’s principle is at work behind the scenes.

This article will dive deep into Bernoulli’s Theorem, its mathematical formulation, key concepts, and real-world applications, making it easier for students, engineers, and curious minds to grasp this vital concept in fluid mechanics.

What is Bernoulli’s Theorem?

Bernoulli’s Theorem states that:

In a steady, incompressible, and non-viscous fluid flow, the total mechanical energy along a streamline is constant.

This energy is composed of:

• Static pressure energy
• Kinetic energy due to velocity
• Potential energy due to elevation

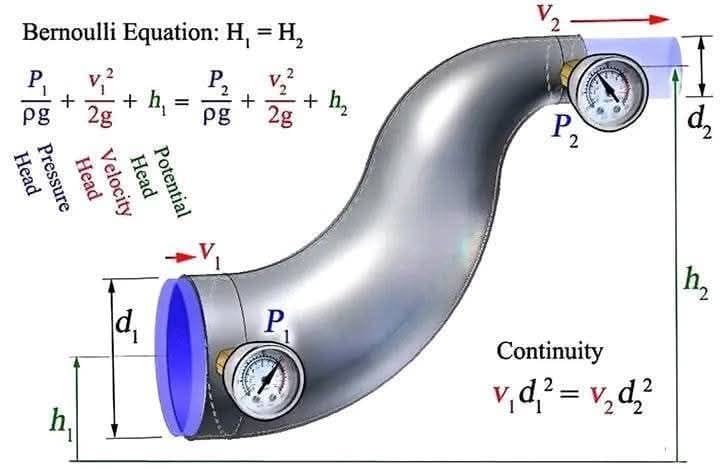
Visual Representation: Understanding Through Diagram

The image below visually demonstrates the flow of fluid through a curved pipe with different diameters. Key elements shown:

• Pressure gauges at two points (P₁ and P₂)
• Heights h₁ and h₂
• Velocities v₁ and v₂
• Diameters d₁ and d₂
• Application of Bernoulli’s equation and continuity principle

As the pipe narrows from d₁ to d₂, velocity increases from v₁ to v₂, and pressure decreases accordingly, illustrating Bernoulli’s theorem in action.

Mathematical Formulation

Where:

• P1​,P2​ = Pressure at point 1 and 2
• v1​,v2​ = Velocity of fluid at point 1 and 2
• h1​,h2​ = Elevation of point 1 and 2 from a reference line
• ρ = Density of the fluid
• g = Acceleration due to gravity
• d1​,d2​ = Diameter at point 1 and 2

This equation is a statement of conservation of energy for flowing fluids.

Key Concepts in Bernoulli’s Equation

1. Static Pressure (P):
   • The pressure exerted by the fluid at rest or in motion.
   • Measured using pressure gauges (as seen in the diagram).
2. Dynamic Pressure (½ρv²):
   • Associated with the fluid’s velocity or kinetic energy.
   • As the fluid speeds up, dynamic pressure increases.
3. Gravitational Potential Energy (ρgh):
   • Related to the height or elevation of the fluid above a reference point.
   • The higher the elevation, the more potential energy the fluid possesses.
4. Streamline:
   • A path that a fluid particle follows.
   • In steady flow, streamlines never cross each other.

Continuity Equation: The Companion to Bernoulli’s Theorem

In fluid flow, mass conservation is key. This is expressed through the Continuity Equation:

A1​v1​=A2​v2​

Or for circular pipes: v₁​d₁²​=v_2​d₂^2​

Where:

• A = Cross-sectional area
• d = Pipe diameter
• v = Fluid velocity

This equation tells us that if the pipe narrows (smaller d), velocity increases, and vice versa.

Conditions for Applying Bernoulli’s Equation

You can apply Bernoulli’s Theorem when the following conditions are met:

• The fluid is incompressible (density is constant).
• The flow is steady (properties at a point do not change with time).
• The fluid is non-viscous (no energy loss due to friction).
• The flow is along a streamline.

Applications of Bernoulli’s Theorem

1. Aircraft Wings (Airfoil Lift Generation)

Airplane wings are curved on the top and flatter at the bottom. Air moving over the top travels faster, reducing pressure due to Bernoulli’s principle. The higher pressure underneath creates lift, allowing the aircraft to fly.

2. Venturi Meter and the Venturi Effect

A Venturi meter is used to measure fluid flow in pipes. It narrows in the middle, causing fluid velocity to increase and pressure to drop. This pressure difference is used to calculate the flow rate.

Venturi Effect: As a fluid passes through a constricted section of pipe, its velocity increases and pressure decreases.

3. Pitot Tube

Used in aviation and fluid velocity measurement. The tube measures the difference between static and stagnation pressure to determine the fluid’s speed using Bernoulli’s equation.

4. Siphons

A siphon allows liquid to flow from a higher elevation to a lower one, even over a barrier. Bernoulli’s theorem explains how the pressure difference due to height helps maintain the flow.

5. Carburetors in Engines

In older engines, a fast airflow through a narrow nozzle (Venturi) draws in fuel due to the pressure drop, mixing air and fuel efficiently before combustion.

6. Spray Bottles and Atomizers

In perfume sprays or insecticide atomizers, squeezing the bottle causes air to speed up through a nozzle, reducing pressure and drawing liquid up the tube.

7. Blood Flow in Arteries

Medical diagnostics use Bernoulli’s principle to understand blood velocity and pressure changes in arteries. Narrowing of blood vessels increases velocity and can indicate blockages.

Conclusion

Bernoulli’s Theorem is a powerful and elegant principle that explains many everyday and industrial phenomena. From airplanes to pipelines, and from medical instruments to fluid transport systems, its applications are vast and significant.

By understanding how energy is conserved in fluid motion, engineers and scientists can design more efficient systems, predict flow behaviors, and solve real-world problems.