A stress-strain curve is a visual representation illustrating how a material behaves under increasing loads. Stress, which is the ratio of force to cross-sectional area, and strain, the ratio of a change in dimension length to the original length, are the defining factors in this graph. These curves can be constructed to examine how materials respond to various loads, such as tension, compression, shear, bending, or torsion. However, this discussion will primarily focus on stress-strain curves generated during tensile loading. Stress-strain curves produced under tension are valuable because they provide engineers with a rapid means of determining several mechanical properties, including the modulus of elasticity (Young’s modulus), yield strength, ultimate strength, and ductility.
A stress-strain curve is generated through a tensile test, where a load is continuously applied to a test specimen until it fractures. The stress experienced by the material is plotted on the Y-axis, while the strain is plotted on the X-axis. This article will define the stress-strain curve, discuss its distinct regions, explain how to interpret it, and highlight its significance in material selection.
What Is Stress?
Stress is a critical factor, refers to the internal resistance or force that a material experiences when subjected to an external load or force. This calculation holds significant importance as it provides engineers with a means to quantify the maximum force a material can withstand before experiencing fracture. Engineers rely on this parameter for the purpose of choosing materials and designing structures that ensure safety and long-term durability. It is typically expressed in units of force per unit area (e.g., Pascals or megapascals in the International System of Units). Stress is a fundamental concept in engineering and materials science and plays a crucial role in understanding how materials respond to external forces.
The symbol used to represent stress is the Greek letter sigma (σ). This symbol is commonly used to denote both normal stress and shear stress.
The formula for stress is depicted below:
Stress = σ = Force/Area
The Pascal (Pa) is the internationally recognized unit for stress in the SI system, although pounds per square inch (psi) is also frequently employed.
What Is Strain?
Strain is a measure of the deformation or change in shape experienced by a material when subjected to an external force or load. It quantifies how much a material’s dimensions change in response to the applied stress. Strain is a dimensionless quantity, typically expressed as a ratio or percentage, and it describes how much a material has stretched, compressed, twisted, or deformed in comparison to its original, undeformed state. The symbol used to represent strain in mechanics and engineering is the Greek letter epsilon (ε).
ε = (∆L) / (L)
where,
ε is strain
∆L is change in length i.e. Final length – Initial length
L is the initial length
Strain is a unitless value since the numbers in both the top and bottom of the formula are in units of length.
What Is the Difference Between Stress and Strain?
Here are the differences between stress and strain:
- Stress pertains to force per unit area, whereas strain concerns the alteration in dimension length relative to the original dimension.
- Stress is quantified in units of Pascals (Pa) or pounds per square inch (psi), while strain is dimensionless.
- Stress is symbolized by 𝛔, and strain is represented by 𝞊.
- Stress is the force responsible for inducing strain.
- Stress is not directly measurable and is computed through mathematical relationships, whereas strain can be directly measured.
Why Is Stress-Strain Curve Important?
The stress-strain curve holds significance as it offers engineers a swift means of extracting a range of paramount mechanical properties for any material. A singular tensile test can generate a stress-strain diagram, enabling the acquisition of the following material properties:
- Young’s modulus
- Yield strength
- Ultimate tensile strength
- Ductility
- Poisson’s ratio
This graphical representation provides a comprehensive snapshot of how a material responds to various loads and helps in material selection and structural design.
How To Make a Stress-Strain Curve?
A stress-strain curve is made by conducting a tensile test using a universal testing machine. The testing machine will automatically capture the data to produce a stress-strain curve as the load increases and the specimen deforms.
How Is the Stress-Strain Curve Measured?
Modern tensile testing machines automatically generate stress-strain curves. These advanced machines continuously monitor and document the force exerted on a test specimen and the resulting deformation it undergoes under that load. The most commonly adopted test procedures for conducting tensile tests and establishing standardized stress-strain curves are those prescribed by ASTM International. For metallic materials, ASTM E8 provides standardization, while ASTM D638 sets the standards for plastic materials. The steps involved in creating a stress-strain curve are outlined in the following list:
- Prepare the test specimen according to the specified dimensions.
- Secure the test specimen within the grips of the tensile testing machine.
- Gradually apply an increasing tensile load to the specimen until it reaches the point of fracture.
- The tensile testing machine will automatically record the stress and strain experienced by the test specimen by monitoring the force applied via the load cell and the displacement of the grips holding the specimen.
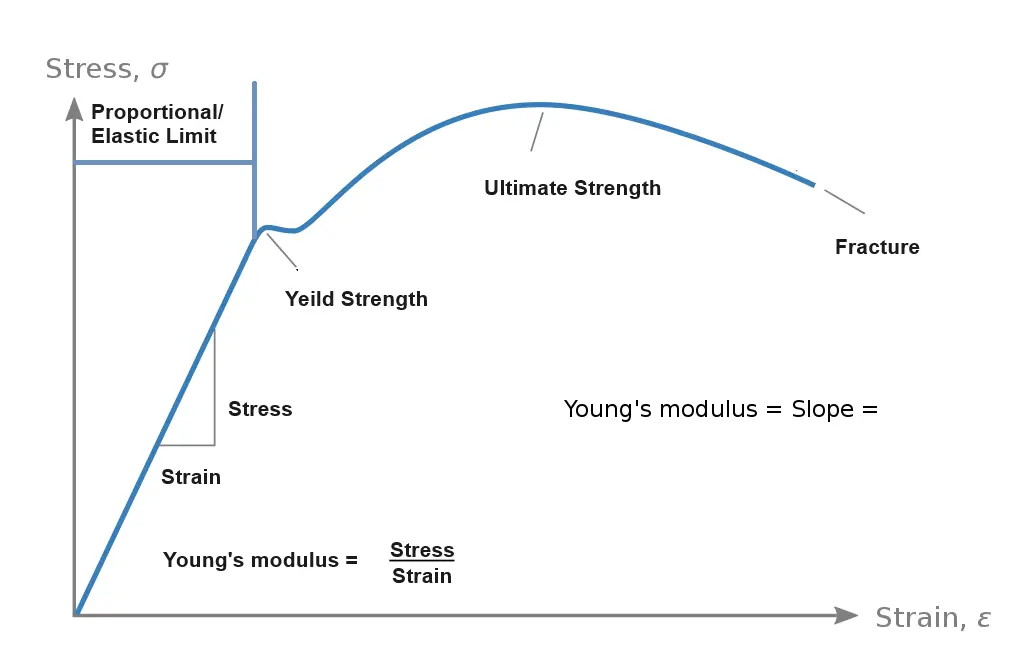
What Are the Different Regions of the Stress-Strain Curve Graph?
The stress-strain curve typically exhibits several distinct stages as a material is subjected to increasing loads. These stages provide valuable information about the material’s behavior. The number of stages and their characteristics can vary depending on the material and its properties, but in general, the following stages are often observed in a stress-strain curve:
1. Proportional Limit
The proportional limit marks the conclusion of the linear segment within the stress-strain curve. All deformation within this limit is characterized by a single constant, known as Young’s modulus, which can be determined by calculating the slope of the stress-strain line up to this point. Young’s modulus is calculated as the ratio of stress to strain in this region.
2. Elastic Limit
The elastic limit represents the specific juncture on the stress-strain curve at which elastic deformation ceases, and plastic deformation commences. Within this limit, if the applied load is relieved at any point, the material will promptly revert to its initial dimensions. In the case of metals, discerning the elastic limit from the proportional limit and the yield point can be challenging due to their close proximity on the curve. Consequently, the elastic limit is typically employed for educational purposes rather than as a practical means of characterizing a material’s properties.
3. Yield Point
The yield point shares similarities with the stress-strain curve’s elastic limit as it demarcates the transition from elastic to plastic deformation. However, the key distinction lies in the methodology used to determine this point. The yield point is a calculated value that accurately specifies the material’s elastic limit or yield strength. It is derived by shifting the linear segment of the stress-strain curve by +0.2% along the horizontal (strain) axis. The point where this offset line intersects with the original stress-strain curve is regarded as the material’s yield strength.
4. Ultimate Stress Point
The ultimate stress point, also known as the ultimate tensile strength, represents the maximum stress encountered in the stress-strain curve. Once the ultimate tensile strength is attained, the test specimen initiates a process known as “necking.” It’s worth noting that although the ultimate stress point is the highest point visible on the stress-strain curve, the actual peak stress value is the true stress at the moment of fracture.
5. Fracture or Breaking Point
The fracture or breaking point on the stress-strain curve signifies the juncture at which the test specimen has undergone significant deformation, leading to the disruption of its microstructure and the eventual fracture of the material.
What Is the Stress-Strain Curve of a Ductile Material?
The stress-strain curve for a ductile material exhibits a distinctive pattern, beginning with a linear increase until it reaches the yield point. Beyond this point, the relationship between stress and strain becomes nonlinear, culminating in a peak at the ultimate tensile strength. Subsequently, the engineering stress decreases nonlinearly as strain continues to rise. Eventually, when the material’s strain surpasses a critical value, it fractures. For additional insights, you can refer to our detailed guide on ductility.
In Figure 1 below, we present an illustration of a stress-strain curve for both ductile and brittle materials as an example:
Stress strain curve Typical carbon steel or mild steel
Engineering Stress and Strain:
Engineering stress and strain are the stress-strain values of material calculated without accounting for the fine details of plastic deformation. These values are also referred to as nominal stress and strain. The values for engineering stress and strain are convenient for measuring the performance of a material and can be directly obtained from a standard tensile test. The formula for engineering stress is shown below:
Engineering Stress Formula (σ) = Force (F) / Original Cross-Sectional Area (A0)
Where:
- σ is the engineering stress (measured in Pascals – Pa or pounds per square inch – psi).
- F is the applied force (measured in Newtons – N or pounds-force – lbf).
- A0 is the original cross-sectional area of the test specimen (measured in square meters – m² or square inches – in²).
The engineering stress represents the force applied to the material divided by its original cross-sectional area and is typically used in the initial linear portion of the stress-strain curve.
The formula for engineering strain is given below:
The formula for engineering strain (ε) is given by:
Engineering Strain Formula (ε) = (Change in Length) / Original Length
Where:
- ε is the engineering strain (dimensionless).
- Change in Length represents the difference between the final length and the original length of the material.
- Original Length is the initial length of the material.
Engineering strain is a unitless measure of how much a material has deformed in relation to its original length. It’s typically used in the initial linear portion of the stress-strain curve.
True Stress and Strain
True stress and true strain are measures of stress and strain that take into account the changing dimensions of a material as it deforms during a tensile test. These values are particularly useful for accurately describing the material’s behavior throughout the entire testing process. The formulas for true stress and true strain are as follows:
True Stress (σ_true):
The true stress is calculated as the ratio of the instantaneous applied force (F) to the instantaneous cross-sectional area (A_i) of the material during deformation. It takes into account the continuously changing area of the specimen as it stretches.
True Stress (σ_true) = F / A_i
Where:
- σ_true is the true stress (measured in Pascals – Pa).
- F is the applied force at the instant in question (measured in Newtons – N).
- A_i is the instantaneous cross-sectional area at the same instant (measured in square meters – m²).
True Strain (ε_true):
The true strain is calculated as the natural logarithm of the ratio of the instantaneous length (L_i) to the original length (L_0) of the material. It accounts for the changing length of the material as it deforms.
True Strain (ε_true) = ln(L_i / L_0)
Where:
- ε_true is the true strain (dimensionless).
- ln denotes the natural logarithm.
- L_i is the instantaneous length at the same instant.
- L_0 is the original length of the material.
True stress and true strain provide a more accurate representation of a material’s behavior during the entire deformation process, particularly in cases where the material undergoes significant changes in dimensions. They are commonly used for materials with nonlinear stress-strain behavior, such as those experiencing necking or significant deformation.
